II L'évolution
du processeur
Abdelwahab Razi
Jusqu'à 1970, les composants d'un processeur ne pouvait pas être contenus dans
un seul circuit intégré, Plusieurs circuits intégrés étaient donc nécessaires.
En 1971, Marcian Hoff, ingénieur chez Intel, trouva le moyen de placer tous les
éléments formant un processeur sur un seul circuit intégré. Il s'agit de la
principale progression menant le processeur à son successeur, le
microprocesseur.
Cette évolution apporte plusieurs améliorations aux processeurs :
•
l'augmentation de la vitesse d'exécution,
•
l'augmentation de sa fiabilité,
•
la réduction de la consommation,
•
la réduction de la taille,
•
et enfin la baisse des prix,
1/
Une progression importante : le microprocesseur
Dans la droite ligne du processeur, le microprocesseur a le même rôle que son
prédécesseur. Cependant, sa rapidité, sa fiabilité et son utilité, entre autres,
se sont grandement renforcés.
a)Une
progression matérielle
Un microprocesseur est constitué de plusieurs unités, dans lesquelles se situent
des sous-unités, qui comprennent à leur tour des sous-unités... Mais les seuls
éléments qui ne comprennent pas de sous-unités constituent l'élément principal
du microprocesseur, le transistor,
-Le transistor
Concrètement, un transistor est un interrupteur capable de relier ou de séparer
deux fils.
Comme tout interrupteur, il peut être dans deux états :
•
passant. Dans ce cas, les deux fils sont reliés et obligatoirement dans le même
état ;
•
non-passant. Les deux fils sont alors séparés, on dit qu'ils sont indépendants,
et ils peuvent être dans un état différent.
L'état du transistor est déterminé par un troisième fil, qui s'adapte aux deux
types de processeurs existants : les processeurs de type P et les processeurs de
type N.
Le premier est également nommé processeur « passant par défaut ». Lorsque son
troisième fil est en état 0, le transistor est passant.
Le second type est appelé « non-passant par défaut », Lorsque le troisième fil
est en état 0, le transistor est non-passant.
Remarque
: Un fil est un élément qui relie les transistors et transmet les informations,
sous forme de «bit», Cette abréviation de « binary digit » est l'unité
fondamentale d'information, Il vaut soit 0, soit 1.

Un transistor est donc un
interrupteur à trois bornes
- Les portes logiques
Une porte logique est un circuit possédant une ou plusieurs entrées, et une ou
plusieurs sorties ; et où l'état d'une sortie dépend uniquement de celui des
entrées.
Les portes logiques simples sont au nombre de six, cependant dans ce TPE, nous
en détailleront seulement cinq, cellesuinous serviront pour la suite, de la plus
simple à la plus compliquée.
La porte « OUI » contient une entrée «a» et une sortie «s». L'état de l'entrée
est tout le temps identique à celui de la sortie.
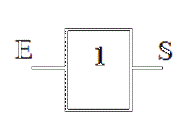
On peut donc établir une formule, dite booléenne : S = E
La porte « NON » a également une entrée «a» et une sortie «s». Plus simplement,
l'état de la sortie s est tout le temps opposé à celui de l'entrée a.
En voici le schéma universel.
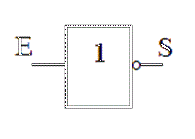
La formule booléenne est donc ici S = Ē
La porte « ET » possède, comme son nom l'indique, deux entrées (a et b), ainsi
qu'une sortie s.
L'état de la sortie est 1 seulement si l'état des deux entrées est également de
1, sinon l'état de la sortie sera de 0.
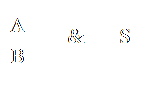
La formule booléenne est ici S = A.B
La porte « OU » donne également sa signification grâce à son nom. En effet,
comme la porte ET, elle possède deux entrées a et b et une sortie s . Cette
dernière est en état 1 seulement si la porte a ou la porte b est en état
1.
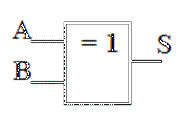
_
_
On peut donc poser S =
(A.B) + (A.B)
Enfin, la porte “DIFF” a une sortie s en état 1 seulement si l'état des deux
entrées a et b sont différents
Entrées
 Sortie
s
Sortie
s
b) Une progression au niveau du fonctionnement
Quel que soit le type de microprocesseur, ce dernier a deux principales
fonctions :
•
Enregistrer des données
•
Transmettre des informations
Pour cela, il va utiliser plusieurs modes de fonctionnement, dont le calcul
binaire et les circuits arithmétiques.
•
Le calcul binaire (ou calcul en base 2 )
Commençons par étudier l'addition en base 2. Cette opération a le même
fonctionnement qu'une addition en base 10, mais avec seulement deux chiffres
possibles : 0 et 1.
Il n'y a donc que trois opérations possibles : 1+1, 1+0 et 0+0.
Les deux dernières opérations donnent le même résultat qu'en base 10, mais 1+1
donne 2 en
base 10, ce qui est impossible en base 2. En calcul binaire, lorsque l'on a 1+1,
on pose 0 et on retient 1.
Voici un exemple d'addition en base 2 :
1 1 0 0 1 0 1
+
1 1 1 0 0 1
____________
1 0 0 1 1 1 1 0
•
Les circuits arithmétiques
1)
Les circuits additionneurs
Le circuit additionneur le plus simple est celui qui additionne deux bits et qui
produit le bit de somme et le bit de retenue. C'est donc un circuit à deux
entrées
a
et
b
et deux sorties
s
et
r
(somme et retenue).
La somme de deux bits donne obligatoiremnt soit 0, soit 1.
Elle est de 0 pour les opérations 0+0 et 1+1. Cependant, pour cette dernière, il
y a une retenue. Le bit de retenue est donc égal à 1. Ici, les états de a et b
sont identiques, on peut donc calculer
r
avec une porte ET.
Elle est de 1 pour l'opération 1+0, Le bit de somme est donc égal à un quand a
et b sont différents, donc on peut calculer s avec une porte DIFF
Comme pour un calcul en base 10, après cette opération, il faut calculer les
deux chiffres suivants, plus une retenue, ce qui nous amène au vrai circuit
additionneur, avec 3 entrées, a, bet c ( la retenue) et deux sorties s et r.
Pour réaliser ce calcul, le plus simple est de séparer cette opération en deux
copies : une une copie pour additionner
a
et
b,
et l'autre pour additionner
c
au bit de somme fourni par la première copie. La retenue totale est égale à 1 si
l'une des copies fournit une retenue égale à 1.
2)
Les circuits soustracteurs
Le circuit soustracteur le plus simple est un circuit à deux entrées
a
et
b
et deux sorties
d
et
r,
qui calcule
a
-
b
et produit en sortie le bit de différence
d
et le bit de retenue
r.
Comme on peut le constater en examinant les 4 cas possibles (0 - 0 = 0, 1 - 0 =
1, 1 - 1 = 0, 0 - 1 = 1 avec une retenue), le bit de différence est égal à 1
quand
a
et
b
sont différents. On peut donc calculer
d
avec une porte DIFF . De même, on constate que
r
est égal à 1 quand
b
et l'inverse de
a
sont égaux à 1. On peut donc calculer
r
avec une porte ET une porte NON .
2/ L'évolution du processeur entraîne celle de l'ordinateur
Le microprocesseur étant le composant principal de l'ordinateur, ses multiples
transformations accélèrent inévitablement l'évolution de l'ordinateur, qui
deviendra un micro-ordinateur, qui correspond à l'ordinateur de bureau
d'aujourd'hui.
a)
Les transformations depuis 1971
De 1971 à 2010, de nombreux microprocesseurs sont sortis.
A chaque nouvelle sortie, il y a une nouvelle évolution, et on constate une
énorme avancée entre ces deeux dates.
La taille s'est réduite, mais la capacité du microprocesseur a fortement
augmenté.
Le tableau ci-dessous est révélateur de cette progression :
|
Date |
Nombre de transistors |
Finesse de gravure (
en µm) |
Largeur de données |
|
1971 |
2300 |
6 |
4 bits |
|
2009 |
774 000
000 |
0,045 |
64 bits |
( La finesse de gravure est la longueur du plus petit fil reliant deux
composants)
Voici le tableau complet des microprocesseurs de 1971 à nos jours.
(MIPS : millions d'instructions effectuées par le processeur par seconde ).
| Date | Nom |
Nombre de transistors |
Finesse de gravure (µm) |
Fréquence de l'horloge |
Largeur des données |
MIPS |
|---|---|---|---|---|---|---|
| 1971 | 4004 | 2 300 | 108 kHz | 4 bits/4 bits bus | ||
| 1974 | 8080 | 6 000 | 6 | 2 MHz | 8 bits/8 bits bus | 0,64 |
| 1979 | 8088 | 29 000 | 3 | 5 MHz | 16 bits/8 bits bus | 0,33 |
| 1982 | 80286 | 134 000 | 1,5 | 6 à 16 MHz (20 MHz chez AMD) | 16 bits/16 bits bus | 1 |
| 1985 | 80386 | 275 000 | 1,5 | 16 à 40 MHz | 32 bits/32 bits bus | 5 |
| 1989 | 80486 | 1 200 000 | 1 | 16 à 100 MHz | 32 bits/32 bits bus | 20 |
| 1993 | Pentium | 3 100 000 | 0,8 à 0,28 | 60 à 233 MHz | 32 bits/64 bits bus | 100 |
| 1997 | Pentium II | 7 500 000 | 0,35 à 0,25 | 233 à 450 MHz | 32 bits/64 bits bus | 300 |
| 1999 | Pentium III | 9 500 000 | 0,25 à 0,13 | 450 à 1 400 MHz | 32 bits/64 bits bus | 510 |
| 2000 | Pentium 4 | 42 000 000 | 0,18 à 0,065 | 1,3 à 3,8 GHz | 32 bits/64 bits bus | 1 700 |
| 2004 | Pentium 4D « Prescott » | 125 000 000 | 0,09 à 0,065 | 2.66 à 3,6 GHz | 32 bits/64 bits bus | 9 000 |
| 2006 | Core 2™ Duo | 291 000 000 | 0,065 | 2,4 GHz (E6600) | 64 bits/64 bits bus | 22 000 |
| 2007 | Core 2™ Quad | 2*291 000 000 | 0,065 | 3 GHz (Q6850) | 64 bits/64 bits bus | 2*22 000 (?) |
| 2008 | Core 2™ Duo (Penryn) | 410 000 000 | 0,045 | 3,33 GHz (E8600) | 64 bits/64 bits bus | ~24 200 |
| 2008 | Core 2™ Quad (Penryn) | 2*410 000 000 | 0,045 | 3,2 GHz (QX9770) | 64 bits/64 bits bus | ~2*24 200 |
| 2008 | Intel Core i7 (Nehalem) | 731 000 000 |
0,045 (2008) 0,032 (2009) |
2,66 GHz (Core
i7 920) 3,33 GHz (Core i7 Ext. Ed. 975) |
64 bits/64 bits bus | ? |
| 2009 | Intel Core i5/i7 (Lynnfield) | 774 000 000 |
0,045 (2009) |
2,66 GHz (Core
i5 750) 2,93 GHz (Core i7 870) |
64 bits/64 bits bus | ? |
-La taille
Grâce à un simple calcul, on peut se rendre compte que si le microprocesseur de
2009 avait la même largeur de données que celui de 1971 ( soit 64 / 8 = 4), il
aurait une finesse de gravure de 0,045 / 8, soit environ 0,006 µm, il serait
donc 1000 fois plus petit qu'en 1971, avec le même nombre de données.
-La vitesse d'exécution
En 1974, le microprocesseur 8080 exécutait 640 000 instructions par seconde alors qu'en 2008, Core 2 Duo en effectue 24 200 000 000, soit environ 38000 fois plus.
b) La loi de Moore
Les lois de Moore sont des énoncés ayant trait à l'évolution des processeurs et
des ordinateurs au cours des années,
Elles au nombre de trois, même si seulement deux d'entres elles ont été
prononcées pas Gordon Moore, un ingénieur de chez “ Fairchild Semiconductor”, un
des trois fondateurs d'Intel.
Ces lois sont plus exactement des conjectures, car à l'époque, ces énoncés n'ont
pas été vérifiées.
Dans le cadre de ce TPE , nous n'étudieront en détail que les deux premières
lois, car la troisième n'est pas très précise, elle n'a d'ailleurs pas d'énoncé
exact.
La première loi de Moore a l'énoncé suivant : la complexité des semi-conducteurs
proposée en entrée de gamme doublera tous les ans. Elle a été prononcée en 1965,
soit 6 ans avant la découverte des microprocesseurs. Cette “loi” était déja mise
en oeuvre depuis 1959, Moore émettait simplement l'hypothèse que cette évolution
allait continuer.
Dix ans plus tard, Moore réévalua cet énoncé, en précisant que le nombre de
transistors par circuit de même taille allait doubler, à prix constants, tous
les dix-huit mois . Cet énoncé, qui n'était qu'une conjecture à l'époque,
acquiert son nom de “loi” car il a été étonnement vérifié de 1971 (invention du
microprocesseur) à nos jours.
Nous allons essayer de vérifier mathématiquement si la loi de Moore est toujours
applicable, grâce au tableau des microprocesseurs (voir plus haut).
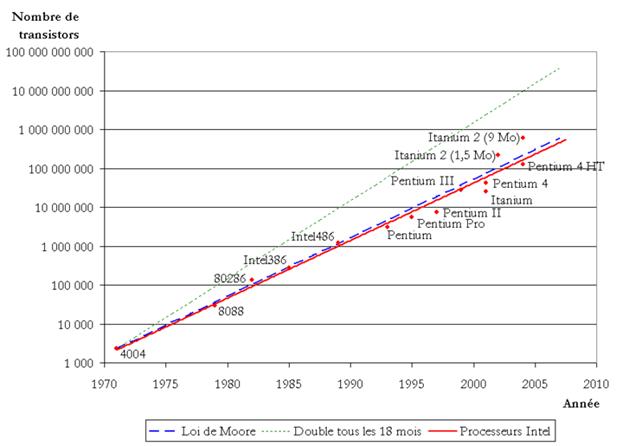
Selon Gordon Moore, le nombre de transistors devait suivre la droite en
pointillés verts. La réalité veut pourtant que les processeurs Intel ( en rouge
), aient moins de transistors que le voudrait la loi de Moore.
Cette loi n'est évidemment pas un loi physique, car elle n'est pas fondée sur
des réalités informatiques, mais dès sa parution, elle est apparue comme un défi
pour les constructeurs, relevé dans les premières années, mais qui s'est heurté
aux effets quantiques et aux désintégrations alpha.
Elle s'est également heurtée à la réalité économique. En effet, la loi du marché
oblige les constructeurs à ralentir la progression pour assurer les ventes aux
classes moyennes.
c) Nouvelles technologies
Grâce à toutes ces évolutions, on a pu assister à la naissance de
“micro-ordinateurs”, les ordinateurs de bureaux dont la première machine a été
vendue en 1972. Aujourd'hui, la quasi-totalité de la population a accès à un
ordinateur.
L'évolution informatique a également entraîné l'invention d'ordinateurs
portables en 1981.
L'évolution a également permis l'invention de microprocesseurs multicoeurs en
2005.
Il s'agit d'un microprocesseur composé de deux unités de calcul. Cette
découverte est due à la demande de plus en plus importante de capacités de
calcul.
Touts les autres progressions comme les fichiers 3D ou multimédia,
l'augmentation du volume des bases de données commencent à dépasser les
capacités d'un microprocesseur à un seul cœur.
Cependant, pour que les microprocesseurs multicoeurs puissent pleinement
exprimer leur potentiel, il faut que les programmes soient adaptés à ce type de
processeurs, donc refaits. En effet, actuellement, très peu de logiciels peuvent
le gérer.
Plusieurs autres projets ont été tentés, comme l'Hyperthreading, qui consiste à
placer deux sous processus sous un processeur, qui peut les gérer simultanément.
Grâce à l'Hyperthreading, le microprocesseur est plus rapide dans ses actions et
ses réactions. Cependant, il a révélé certains défauts, il permet d'accéder à
des informations d'autres thread, donc d'autres ordinateurs.